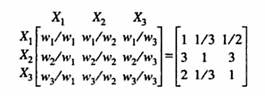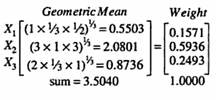Respondents were asked to rate the various factors on a scale. These ratings were converted into importance weights (percentage weights summing up to 100 per cent).
A respondent assesses n(n-1)/ 2 importance ratios between attributes. This information is stored in the upper (or lower) triangle of a (n x n) matrix, whose typical element ajk represents the weight ratio of wi/wk. The remaining elements of the matrix are filled by employing the reciprocal of the matrix: ajk = 1/akj and ajj = 1, for all j and k.
Example: The following pair wise judgments were made
We compute the geometric mean of each row of the matrix and then normalise the resulting numbers:
The ratings of each respondent are converted into weights. For a given segment of the sample of respondents, the mean weights for every factor are then computed.